Thursday, October 29, 2009
Calvinism, According to Custardy
I like this guy's explanation of TULIP: http://custardy.blogspot.com/2009/10/calvinism.html. Of the few who read my blog, I think the majority are Reformed. What do you all think of it?
Labels:
short
Saturday, August 08, 2009
Essays!
Here's some recommended reading; several essays, articles & such that I've read at one time or another and found to be especially illuminating or memorable:
The Problem With Music, by Steve Albini
An enlightening look at the relationship between new bands and record labels. I used to want to be a rock musician. This essay confirmed to me that I should be an indie rock musician, if anything. I eventually gave that up because there was no money in it and I didn't have the ability or motivation to write songs, but that's another thing.
I, Pencil, by Leonard E. Read
A testament to the creative power of free market economies.
Fern-Seed and Elephants, by C.S. Lewis
C.S. Lewis, as a literary critic, rips on the methods of some Biblical critics.
The Special Theory of Relativity, by Richard Feynman
This is best explanation of Special Relativity I've ever encountered. I think that is because 1. He starts with Newton's physics, which I understand, and compares it to Special Relativity, and 2.
He uses math. Math is hard and boring and scary, so some explanations try to avoid it, relying on imagination alone, and fail miserably. Maybe because modern physical theories are mathematical statements. Don't fight it! Give in to the algebra. Listen to the calculus.
Parkinson's Law, by C. Northcote Parkinson
On second reading, I think the title is immodest and the article is a bit tongue-in-cheek, but it's nonetheless convincing. I bet Parkinson's Law applies to corporate managers, but it's counteracted by the fact that laying off excess managerial staff is a good way to cut costs.
The Myth of Sisyphus, by Albert Camus
I generally like the famous existentialist writers, even though I disagree with them on some very basic things. Maybe it's because we ask the same questions, though we accept different answers. This essay has popped into my mind many times since I first read it years ago.
G.K. Chesterton
Chesterton gets his own section. He's sophistical at times, but his insight and his humor are priceless. These are a few of my favorites.
The Problem With Music, by Steve Albini
An enlightening look at the relationship between new bands and record labels. I used to want to be a rock musician. This essay confirmed to me that I should be an indie rock musician, if anything. I eventually gave that up because there was no money in it and I didn't have the ability or motivation to write songs, but that's another thing.
I, Pencil, by Leonard E. Read
A testament to the creative power of free market economies.
Fern-Seed and Elephants, by C.S. Lewis
C.S. Lewis, as a literary critic, rips on the methods of some Biblical critics.
The Special Theory of Relativity, by Richard Feynman
This is best explanation of Special Relativity I've ever encountered. I think that is because 1. He starts with Newton's physics, which I understand, and compares it to Special Relativity, and 2.
He uses math. Math is hard and boring and scary, so some explanations try to avoid it, relying on imagination alone, and fail miserably. Maybe because modern physical theories are mathematical statements. Don't fight it! Give in to the algebra. Listen to the calculus.
Parkinson's Law, by C. Northcote Parkinson
On second reading, I think the title is immodest and the article is a bit tongue-in-cheek, but it's nonetheless convincing. I bet Parkinson's Law applies to corporate managers, but it's counteracted by the fact that laying off excess managerial staff is a good way to cut costs.
The Myth of Sisyphus, by Albert Camus
I generally like the famous existentialist writers, even though I disagree with them on some very basic things. Maybe it's because we ask the same questions, though we accept different answers. This essay has popped into my mind many times since I first read it years ago.
G.K. Chesterton
Chesterton gets his own section. He's sophistical at times, but his insight and his humor are priceless. These are a few of my favorites.
Labels:
G.K. Chesterton,
philosophy,
recommended reading
Thursday, July 02, 2009
Alternative Hexadecimal Digits
I'm not complaining about the convention of using characters 0-9 and A-F as hexadecimal digits. It's a good system; it's easy to learn, since most of us in the Western World have known the meaning of 0-9 and the order of the alphabet since childhood. But what if we could start over with only practical concerns (apart from the value of keeping a well-recognized and heavily-used convention) to guide us?
I can think of a few desirable traits for a set of hexadecimal digits:
In handwritten form:
 For LCD/LED displays:
For LCD/LED displays:
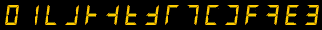
Description of This Alternative
First off, the digits for zero and one are the same as in conventional binary, octal, and decimal.
Next, a definition: the binary composition of a number is the set of integral powers of 2 that add up to that number. For example, the binary composition of 76 is the set {64, 8, 4} or {26, 23, 22}, since its members are integral powers of 2 and they add to 76.
With this definition in mind, the following are true of the alternative digit for a given number 1-15:
Some Benefits of This Alternative
Because of these rules, if a hexadecimal digit is depicting a nibble of memory (e.g. in a hex dump program), one only has to look at a certain part of the digit to see if a particular bit is set to 1 or 0. Also, those of you who know about electronic logic gates can tell that the circuitry needed to take a four-bit input representing a number and light up the proper parts of an LED/LCD digit display would be a bit simpler these digits than with the conventional digits.
Update: I've been collaborating with Valdis Vītoliņš on a new set of alternative hexadecimal digits. They are an improvement on the digits described in this post. See this blog post.
I can think of a few desirable traits for a set of hexadecimal digits:
- They should be easy to learn.
- It should be easy to write them by hand quickly without them being ambiguous or difficult to read.
- They should be representable using the common LCD/LED displays used in clocks, calculators, etc.
- They should depict their binary counterparts somehow. In software, we must sometimes translate between hexadecimal and binary, e.g. to determine whether a given bit in a given word is 1 or 0. If the oneness or zero-ness of each bit in a nibble was visibly represented in its corresponding digit, this translation would be easier.
In handwritten form:
 For LCD/LED displays:
For LCD/LED displays: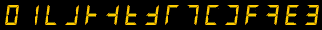
Description of This Alternative
First off, the digits for zero and one are the same as in conventional binary, octal, and decimal.
Next, a definition: the binary composition of a number is the set of integral powers of 2 that add up to that number. For example, the binary composition of 76 is the set {64, 8, 4} or {26, 23, 22}, since its members are integral powers of 2 and they add to 76.
With this definition in mind, the following are true of the alternative digit for a given number 1-15:
- If one is part of a number's binary decomposition, its digit faces right otherwise it faces left. Equivalently, the digits for even numbers face the same direction as 'e' and 'n', and the digits for odd numbers face the same direction as 'd'.
- The digit has a stroke across its base if and only if two is part of the number's binary composition.
- The digit has a stroke across its middle if and only if four is part of the number's binary composition.
- The digit has a stroke across its top if and only if eight is part of the number's binary composition.
Some Benefits of This Alternative
Because of these rules, if a hexadecimal digit is depicting a nibble of memory (e.g. in a hex dump program), one only has to look at a certain part of the digit to see if a particular bit is set to 1 or 0. Also, those of you who know about electronic logic gates can tell that the circuitry needed to take a four-bit input representing a number and light up the proper parts of an LED/LCD digit display would be a bit simpler these digits than with the conventional digits.
Update: I've been collaborating with Valdis Vītoliņš on a new set of alternative hexadecimal digits. They are an improvement on the digits described in this post. See this blog post.
Labels:
hexadecimal numbers
Sunday, June 21, 2009
Spice Rack

Parts:
- 2 boards: 36" long and about 3-1/2"
- 23 dowels: 36" long and 1/4" diameter
- 4 metal angle brackets
- Mallet
- Drill
- 30/60/90 triangle (like for geometry class)
- Ruler or tape measure
- C-clamps
- 1/4" wood drill bit
- Small drill bit (for pre-drilling screw holes)
- Screwdriver
- Saw (and a saw box, if you have one)
- Level
- On the pattern below, the X's represent the centers of drill holes. Each small square is 1/4" long. Draw this pattern onto the end of one of the boards using the 30/60/90 triangle. The left side of the diagram corresponds to the front side of the spice rack.
- Repeat the pattern 4-1/2" apart for each row in the rack.
- Clamp the two boards together with the drawn pattern visible on top.
- Drill 1/4" holes centered on each X drawn.
- Saw the dowels in half.
- Stain or paint the boards and dowels, if you want to.
- Pound the dowels into the drill holes.
- Screw the angle brackets onto the boards so they are flush with the back of the spice rack.
- Screw the angle brackets onto the door. Make it level, of course.
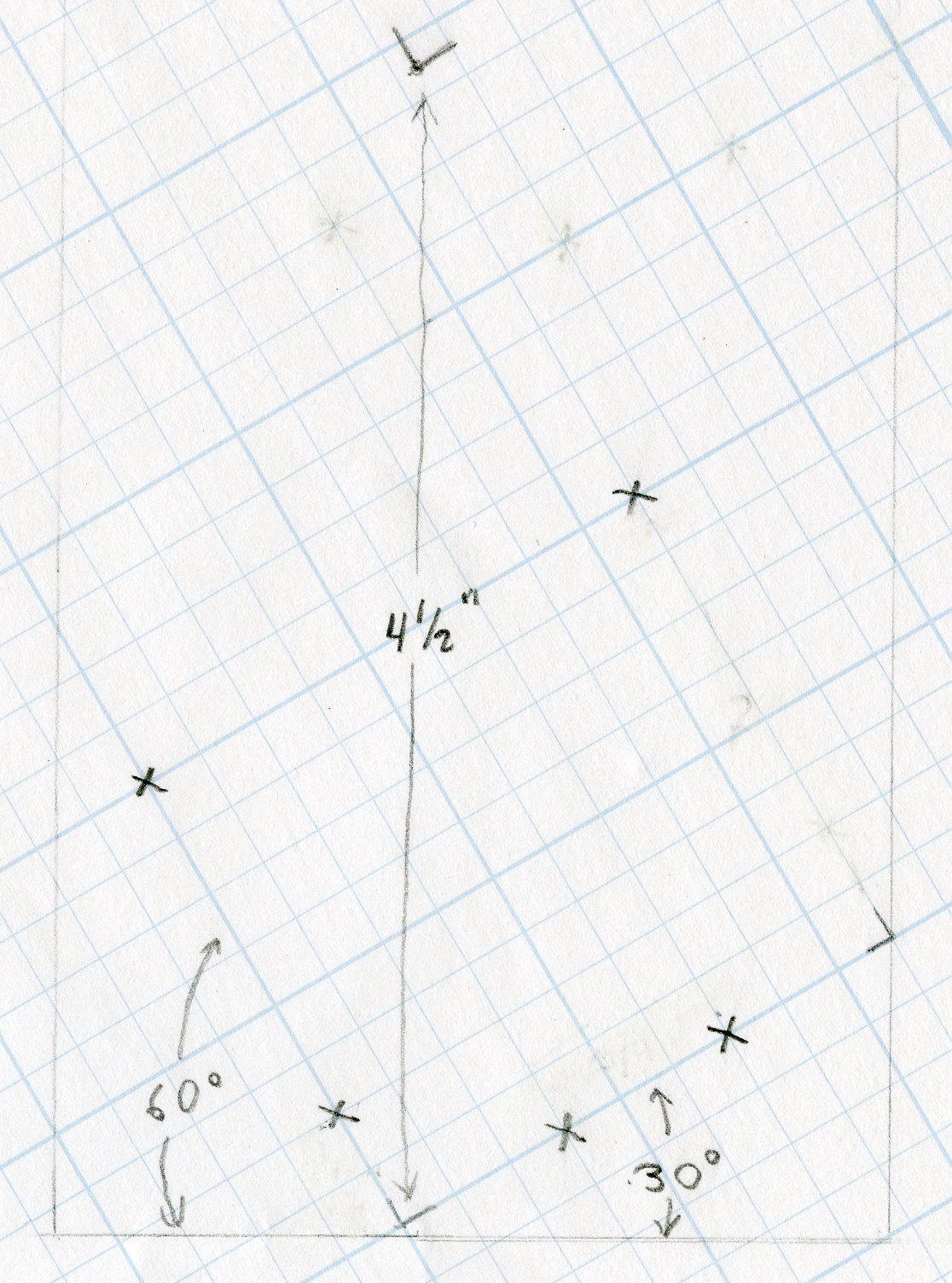
Notes:
- Make sure hole for the dowels are drilled at a straight 90 degrees, so the dowels don't go in crooked.
- When drilling holes through the two boards, press some scrap wood against where the drill bit will go out the other side, to prevent the bottom board from splintering.
- If the dowels are are the same size or bigger than the holes, you won't need glue to hold the rack together.
- It's easier to stain the rack before putting it together than after.
Labels:
DIY,
spice racks
Thursday, June 04, 2009
Somebody's Wrong
- Fact: I say someone is wrong about something.
- It follows then that someone is wrong about something. This is proven indirectly:
- Assume everyone is correct about everything. If so, then the statement I have made in (1) is wrong.
- Since the statement I made in (1) is wrong, someone is wrong about something.
- (2.1) and (2.2) contradict each other.
Therefore, someone is wrong about something. - Furthermore, that wrong idea is not what I said in statement (1). Proof of this is as follows:
- (2) proves that someone is wrong about something.
- Since someone is wrong about something, my statement that someone is wrong about something is true and thus not wrong.
Therefore, there is at least one wrong idea held by at least one person, and it is not my statement that someone is wrong about something.
Labels:
logic
Sunday, May 31, 2009
Samuel Johnson's A Journey to the Western Islands of Scotland in Google Earth
Here it is, finally, after talking about it so much. I've mapped Samuel Johnson's A Journey to the Western Islands of Scotland in Google Earth. You can download it either as a KMZ or as a KML file. The KML file is much smaller, but it will load more slowly since the images it uses are online rather than embedded in the file. I recommend using the KMZ file.
I welcome corrections and additions, especially with regards to the identification of places and landmarks, so long as a rationale is given. I'm no historian, but I would like to make this thing accurate.

I welcome corrections and additions, especially with regards to the identification of places and landmarks, so long as a rationale is given. I'm no historian, but I would like to make this thing accurate.

Labels:
KML,
Samuel Johnson,
UK
Subscribe to:
Comments (Atom)


