- Instead of showing just one counterexample, clicking the "Counterexample" button more than once causes the application to cycle through different counterexamples for the current statement.
- There is a new button: the "Example" button, which is the opposite of the "Counterexample" button.
- Propositions (nullary predicates) can now be lower-case letters as well as upper-case letters.
- There is now a "therefore" operator -- ',' -- apostrophe comma apostrophe, for representing logical arguments.
Showing posts with label UPL. Show all posts
Showing posts with label UPL. Show all posts
Saturday, March 31, 2018
Improvements to somerby.net/mack/logic
After a spate of good input from commenters, I've improved somerby.net/mack/logic in several ways:
Sunday, April 17, 2016
A Cancel Button for somerby.net/mack/logic
Good news: somerby.net/mack/logic now has a cancel button. If a decision is taking too long, you can cancel it and continue working. You don't have to close the browser anymore.
Bad news: somerby.net/mack/logic is not working in Internet Explorer, or at least it isn't working in Internet Explorer 11 on my computer. I'll try to fix it soon.
It works for me in Chrome and Firefox. I'd appreciate it if anyone tells me whether or not its working for them in other browsers. Just leave a comment on this post.
Bad news: somerby.net/mack/logic is not working in Internet Explorer, or at least it isn't working in Internet Explorer 11 on my computer. I'll try to fix it soon.
It works for me in Chrome and Firefox. I'd appreciate it if anyone tells me whether or not its working for them in other browsers. Just leave a comment on this post.
Saturday, July 11, 2015
Binary Operators in somerby.net/mack/logic
Binary Operators in somerby.net/mack/logic now have different precedences. See here.
Labels:
UPL
Sunday, May 03, 2015
Counterexample Feature Completed for somerby.net/logic
The "Counterexample" button now works for modal statements as well as non-modal statements in somerby.net/mack/logic.
Labels:
UPL
Tuesday, April 14, 2015
Addtions to somerby.net/mack/logic
I added operators for strict implication and definite description to somerby.net/mack/logic. I also added the beginnings of a feature that finds counterexamples for statements that are not necessarily true. It only works for non-modal statements, but I think I can expand it to work for modal statements as well.
Labels:
UPL
Saturday, March 28, 2015
Free Variables Are Back (partially)
I've added some support for free variables back into somerby.net/mack/logic. They are now treated as constants denoting actual objects. At the moment, they are not allowed in statements which contain modal operators, since I have not yet found a satisfactory way to deal with constants in modal statements. Or at least a way that I'm willing to commit to. I'm working on it. I've been reading Possible Worlds, "Actualism" and "SQML" and other such things for instruction and insight. I knew that there was more than one system of modal logic, but this reading has made me appreciate the need for me to define exactly what system of modal logic somerby.net/mack/logic implements. So I'm working on that, too.
Labels:
UPL
Friday, February 13, 2015
No More Free Variables (for now)
Formerly, somerby.net/mack/logic would accept statements with free variables. It would bind them all with existential quantifiers. That seemed to work; it yielded the results I expected for all of the statements I had tried - up until a few days ago, when I found it to fail for some statements. One such statement is "a=b". I would expect this to be a contingent statement; true or false depending on whether or not a and b denoted the same object, but the application decided it to be necessarily true. It's not hard to see why if we expand the statement, as the application does, to be "3b,3a,a=b". There is always an a and a b which are identical in any nonempty universe; they are identical when they are the same object.
So, for now, the application rejects statements that contain free variables. I'm working on finding a way to decide them correctly. As soon as I've found one (and I've assured myself that it really is correct), I'll incorporate it into the application and allow free variables once again.
So, for now, the application rejects statements that contain free variables. I'm working on finding a way to decide them correctly. As soon as I've found one (and I've assured myself that it really is correct), I'll incorporate it into the application and allow free variables once again.
Labels:
UPL
Saturday, January 24, 2015
Another Square of Opposition
In my former post, I showed Terrence Parsons' theory of Aristotle's Square of Opposition in symbolic form. I also noted that the Square of Opposition holds up under the modern interpretation of the four forms of Term Logic if it is assumed a priori that the subject terms of the forms is non-empty (I am not the first to note this; see section 2.2.2 of iLogic). So there are two interpretations of the four forms which affirm the Square of Opposition. But are there others?
I found another interpretation of the four forms of Term Logic that affirms the Square of Opposition. It's a parallel to Parsons' Square. Parson constructs the square by taking the modern interpretation of the four forms, bestowing existential import upon Form A and denying existential import to the form on the opposite corner - Form O. The interpretation I found is constructed by by taking the modern interpretation of the four forms, bestowing existential import upon Form E, and denying existential import to Form I on the opposite corner. Here is a statement of it in symbolic form:
I'd like know if anyone else has thought of it before.
This interpretation, like Parsons' interpretation and the modern interpretation combined with a non-empty subject term, affirms the Logical Hexagon:
I found another interpretation of the four forms of Term Logic that affirms the Square of Opposition. It's a parallel to Parsons' Square. Parson constructs the square by taking the modern interpretation of the four forms, bestowing existential import upon Form A and denying existential import to the form on the opposite corner - Form O. The interpretation I found is constructed by by taking the modern interpretation of the four forms, bestowing existential import upon Form E, and denying existential import to Form I on the opposite corner. Here is a statement of it in symbolic form:
// Another Square of Opposition // "All S are P", with no existential import A <=> (x,Sx->Px) // "No S are P", with existential import E <=> ((x,Sx->~Px)&(3x,Sx)) // "Some S are P", with no existential import // "If there are any S, some of them are P" might be a better way to state it. I <=> ((3x,Sx)->(3x,Sx&Px)) // "Some S are not P" under the modern interpretation with existential import // Since it has existential import, there's no need to state is as "Not all S are P". O <=> ~(x,Sx->Px) -> // Contraries ~(A&E) // Contradictories A ^ O I ^ E // Subcontraries I | O // Subalterns A -> I E -> O
I'd like know if anyone else has thought of it before.
This interpretation, like Parsons' interpretation and the modern interpretation combined with a non-empty subject term, affirms the Logical Hexagon:
// The Logical Hexagon: // "All S are P", with no existential import A <=> (x,Sx->Px) // "No S are P", with existential import E <=> ((x,Sx->~Px)&(3x,Sx)) // "Some S are P", with no existential import // "Some S are P, if any S exist" is a better way to state it. I <=> ((3x,Sx)->(3x,Sx&Px)) // "Some S are not P", existential import // Since it has existential import, there's no need to state is as "Not all S are P". O <=> ~(x,Sx->Px) // The statement U may be interpreted as "Either all S are P or all S are not P." U <=> ((x,Sx->Px)|(x,Sx->~Px)) // The statement Y may be interpreted as "Some S is P and some S is not P" Y <=> ((3x,Sx&Px)&(3x,Sx&~Px)) -> // Subalterns: AI, AU, EU, EO, YI, YE A->I A->U E->U E->O Y->I Y->O // Contraries: AE, EY, YA ~(A&E) ~(E&Y) ~(Y&A) // Subcontraries: IU, UO, OI I|U U|O O|I // Contradictories: AO, UY, EI A^O U^Y E^I
Labels:
logic,
philosophy,
UPL
Thursday, January 01, 2015
A Second Theory of Term Logic
I added Term Logic to somerby.net/mack/logic for fun. While doing the necessary research, I discovered the logical Square of Opposition, which is kind of cool. Terence Parsons wrote an illuminating article on the Square. In it, he argues convincingly for an interpretation of 2-term propositions that affirms the Square of Opposition, and also convincingly that this interpretation is Aristotle's intended interpretation. I like the article so much that I've chosen to use this interpretation in my application, defining the four forms of propositions (SaP, SeP, SiP, SoP) just as he does. Even so, I doubt that this is the only coherent theory of Term Logic held by premodern logicians. Here I shall explain why. You can click on any of the symbolic statements in this post to test them in somerby.net/mack/logic.
When explaining why the interpretation of the O-form as "Some S is not P" did not cause problems for premodern logicians, Parsons dismisses the possibility that they assumed that the S-term was not empty, stating "Explicitly rejecting empty terms was never a mainstream option, even in the nineteenth century". But I'm not so sure. First of all, just because they did not explicitly reject empty terms does not mean they implicitly rejected empty terms. Second, they did not have to reject empty terms altogether to make this interpretation of O-form compatible with the traditional Square of Opposition. They only needed to assume a priori (and perhaps unconsciously) that the S-term was not empty whenever they were making an argument. This isn't a very rigorous thing to do, but it's a natural thing to do. Usually, if we are making assertions about some kind of thing, it's because some such thing exists and we want to say something meaningful about it. Reasoning about unicorns may have its uses, but they are not obvious.
Suppose that some pre-modern philosophers, like Boethius and Peter of Spain, did not interpret the propositional forms as Aristotle intended. Instead, they assumed a priori that the S-term was nonempty, and let the O-form have existential import, just as Boethius seemed to be doing when he translated "Some S is P". Then, instead of the Square of Opposition being this:
they believed the Square of Opposition was this:
The relationships of the Square hold in this interpretation as well as in Aristotle's.
And then there is the matter of the Principle of Obversion and the Principle of Contraposition. Parsons says that some medieval logicians advocated these principles, though they are both fallacious under Aristotle's interpretation of the four forms. The following is not necessarily true:
This is not necessarily true, either:
Why did some logicians make these mistakes? And why did other logicians like Peter of Spain endorse them? Maybe to them, they weren't mistakes. Under what we call the modern interpretations of the four forms, these principles are necessarily true.
Being necessarily true, they will still, of course, be true under an a priori assumption that the S-term is nonempty. So maybe there was a theory of term logic floating around Medieval Europe that looked like this:
If so, then they really did have a coherent theory of Term Logic which affirmed the Principle of Conversion by Contraposition and the Principle of Obversion. I can't be sure, since I haven't looked for evidence to the contrary, e.g. Peter of Spain discussing empty terms in Summulae Logicales Magistri Petri Hispani, but as far as I know, it makes sense. I guess I'll have to read some Medieval logic to find out. It's too bad I don't know Latin.
When explaining why the interpretation of the O-form as "Some S is not P" did not cause problems for premodern logicians, Parsons dismisses the possibility that they assumed that the S-term was not empty, stating "Explicitly rejecting empty terms was never a mainstream option, even in the nineteenth century". But I'm not so sure. First of all, just because they did not explicitly reject empty terms does not mean they implicitly rejected empty terms. Second, they did not have to reject empty terms altogether to make this interpretation of O-form compatible with the traditional Square of Opposition. They only needed to assume a priori (and perhaps unconsciously) that the S-term was not empty whenever they were making an argument. This isn't a very rigorous thing to do, but it's a natural thing to do. Usually, if we are making assertions about some kind of thing, it's because some such thing exists and we want to say something meaningful about it. Reasoning about unicorns may have its uses, but they are not obvious.
Suppose that some pre-modern philosophers, like Boethius and Peter of Spain, did not interpret the propositional forms as Aristotle intended. Instead, they assumed a priori that the S-term was nonempty, and let the O-form have existential import, just as Boethius seemed to be doing when he translated "Some S is P". Then, instead of the Square of Opposition being this:
// Aristotle's Square of Opposition A <=> ((x,Sx->Px) & (3x,Sx)) E <=> (x,Sx->~Px) I <=> 3x,Sx&Px O <=> ((3x,Sx&~Px)|(~3x,Sx)) -> // Contraries ~(A&E) // Contradictories A ^ O I ^ E // Subcontraries I| O // Subalterns A -> I E -> O
they believed the Square of Opposition was this:
// A Hypothetical Alternative to // Aristotle's Square of Opposition 3x,Sx // Assume a priori that S is not empty. A <=> (x,Sx->Px) // (Existential import here would be redundant.) E <=> (x,Sx->~Px) I <=> (3x,Sx&Px) O <=> (3x,Sx&~Px) // Assume O has existential import. -> // Contraries ~(A&E) // Contradictories A ^ O I ^ E // Subcontraries I | O // Subalterns A -> I E -> O
The relationships of the Square hold in this interpretation as well as in Aristotle's.
And then there is the matter of the Principle of Obversion and the Principle of Contraposition. Parsons says that some medieval logicians advocated these principles, though they are both fallacious under Aristotle's interpretation of the four forms. The following is not necessarily true:
// The Principle of Conversion by Contraposition, // with Aristotle's interpretation // of the A-form and the O-form ((x,Sx->Px) & (3x,Sx)) <=> ((x,~Px->~Sx) & (3x,~Px)) ((3x,Sx&~Px)|(~3x,Sx)) <=> ((3x,~Px&~~Sx)|(~3x,~Px))
This is not necessarily true, either:
// The Principle of Obversion, // with Aristotle's interpretation // of the A-form and the O-form // Every S is P = No S is non-P (SaP <=> Se~P) ((x,Sx->Px) & (3x,Sx)) <=> (x,Sx->~~Px) // No S is P = Every S is non-P (SeP <=> Sa~P) (x,Sx->~Px) <=> ((x,Sx->~Px) & (3x,Sx)) // Some S is P = Some S is not non-P (SiP <=> So~P) (3x,Sx&Px) <=> ((3x,Sx&~~Px)|(~3x,Sx)) //Some S is not P = Some S is non-P (SoP <=> Si~P) ((3x,Sx&~Px)|(~3x,Sx)) <=> (3x,Sx&~Px)
Why did some logicians make these mistakes? And why did other logicians like Peter of Spain endorse them? Maybe to them, they weren't mistakes. Under what we call the modern interpretations of the four forms, these principles are necessarily true.
// The Principle of Conversion by Contraposition, // with the modern interpretations of the forms: (x,Sx->Px) <=> (x,~Px->~Sx) (3x,Sx&~Px) <=> (3x,~Px&~~Sx)
// The Principle of Obversion, // with the modern interpretations of the forms: // Every S is P = No S is non-P (SaP <=> Se~P) (x,Sx->Px) <=> (x,Sx->~~Px) // No S is P = Every S is non-P (SeP <=> Sa~P) (x,Sx->~Px) <=> (x,Sx->~Px) // Some S is P = Some S is not non-P (SiP <=> So~P) (3x,Sx&Px) <=> (3x,Sx&~~Px) //Some S is not P = Some S is non-P (SoP <=> Si~P) (3x,Sx&~Px) <=> (3x,Sx&~Px)
Being necessarily true, they will still, of course, be true under an a priori assumption that the S-term is nonempty. So maybe there was a theory of term logic floating around Medieval Europe that looked like this:
3x,Sx A <=> (x,Sx->Px) E <=> (x,Sx->~Px) I <=> (3x,Sx&Px) O <=> (3x,Sx&~Px) -> // Contraries ~(A&E) // Contradictories A ^ O I ^ E // Subcontraries I | O // Subalterns A -> I E -> O
If so, then they really did have a coherent theory of Term Logic which affirmed the Principle of Conversion by Contraposition and the Principle of Obversion. I can't be sure, since I haven't looked for evidence to the contrary, e.g. Peter of Spain discussing empty terms in Summulae Logicales Magistri Petri Hispani, but as far as I know, it makes sense. I guess I'll have to read some Medieval logic to find out. It's too bad I don't know Latin.
Labels:
logic,
philosophy,
UPL
Friday, November 28, 2014
Feedback for somerby.net/mack/logic
Anyone who wishes to comment on somerby.net/mack/logic, please leave your comments here.
Saturday, March 29, 2014
Investigating Logical Arguments with somerby.net/mack/logic
I created a web application that evaluates logical arguments. To provide an example of how it might be used, I'm going to use it to help me do a brief investigation of two modal arguments about the existence of God. The first is Alvin Plantinga's modal argument for the existence of God. The second is Juan Manuel Correa's counter-argument against the existence of God (or at least against the soundness of Plantinga's argument). Statements of both arguments can be found on Wikipedia at http://en.wikipedia.org/wiki/Ontological_argument#Alvin_Plantinga.
First off, I'm going to strip the arguments down to what I think is the essential logic that makes both arguments work. I don't suppose this will be agreeable to everyone, at least not without some persuasion, but I'll just go with it for now and try to defend myself later if I have to. So, for Plantinga's argument I will use:
Before I try to answer that question, I want to check that neither argument is trivially valid. I mean, I want to be sure that neither conclusion follows from its premises simply because those premises contain a contradiction and anything follows from a contradiction. So I test the premises by themselves in the decider.
So, to conclude, I will assert 1. that God exists in some possible world. 2. There is a possible world where God doesn't exist. Therefore, Premise #1 is false.
To summarize my reasoning in symbolic form:
The decider confirms that this argument is valid.
One more thing I'd like to point out: when considering modal arguments for the existence of God, one should be careful about the statement "It is possible that God exists." It might be interpreted two different ways. First, as "there is a possible world in which God exists". The second, as "I don't know anything that precludes the existence of God." The first is easy to represent in terms of modal logic, but the second is the more natural interpretation. In my analysis, I assumed the first. If I were to choose the second interpretation, my analysis of these two arguments would have to be different.
First off, I'm going to strip the arguments down to what I think is the essential logic that makes both arguments work. I don't suppose this will be agreeable to everyone, at least not without some persuasion, but I'll just go with it for now and try to defend myself later if I have to. So, for Plantinga's argument I will use:
<>G->[]G <>G -> GWhich is saying,
- If God exists in some possible world, God exists in every possible world.
- There is a possible world in which God exists.
- Therefore, God exists.
<>G->[]G <>~G -> ~GWhich is saying,
- If God exists in some possible world, God exists in every possible world.
- There is a possible world in which God does not exist.
- Therefore, God does not exist.
<>G->[]G <>G <>~GIt tells me they are impossible, i.e. logically inconsistent with each other. So we can't believe all of them at once. Which one should I doubt?
Before I try to answer that question, I want to check that neither argument is trivially valid. I mean, I want to be sure that neither conclusion follows from its premises simply because those premises contain a contradiction and anything follows from a contradiction. So I test the premises by themselves in the decider.
<>G->[]G <>GThen
<>G->[]G <>~GThe decider says both pairs are contingent. So no problem there. What about the two differing premises? The decider says
<>G & <>~Gis possible, which it just what I expect, so I could believe both. Which is what I'm inclined to do. I can imagine a world with God, and I can imagine a world without God. Of course, just because I can imagine them doesn't mean that there is not some contradiction hiding in either conception. But I'm still most inclined to drop Premise #1. It's obvious that []G and <>~G are incompatible, and it's not clear to me that there ever could be such a thing as a necessary being. Some logics entail that at least one being must exist; See Proposition 24.52 in Principia Mathematica for one. Even so, just because you can prove that at least one object exists doesn't mean you can prove that it has any nontrivial properties, like divinity. And I'm not enamoured of the idea that God has every possible perfection; necessary being being one of those perfections. Clearly, if a being has every possible perfection, it must smell like freshly-baked chocolate chip cookies at least some of the time. And play a face-melting guitar solo every time it picks up a guitar. Unless someone is taking a nap within earshot. But I'm a Christian, and I'm sure both of these perfections are irrelevant to the Gospel, so I don't care.
So, to conclude, I will assert 1. that God exists in some possible world. 2. There is a possible world where God doesn't exist. Therefore, Premise #1 is false.
To summarize my reasoning in symbolic form:
<>G <>~G []( (<>G&P) -> C ) []( (<>~G&P) -> ~C ) -> ~PWhere P is premise #1, C is the conclusion of Plantinga's argument, and G is as defined above.
The decider confirms that this argument is valid.
One more thing I'd like to point out: when considering modal arguments for the existence of God, one should be careful about the statement "It is possible that God exists." It might be interpreted two different ways. First, as "there is a possible world in which God exists". The second, as "I don't know anything that precludes the existence of God." The first is easy to represent in terms of modal logic, but the second is the more natural interpretation. In my analysis, I assumed the first. If I were to choose the second interpretation, my analysis of these two arguments would have to be different.
Saturday, February 01, 2014
somerby.net/mack/logic
Here's a web application that decides simple statements in a fragment of first-order symbolic logic: somerby.net/mack/logic. It's based on that .NET console application I was calling "Monadic Predicate Logic".
Monday, October 31, 2011
Monadic Predicate Logic with Some Modal Operators
I have a new version of the monadic predicate logic program that I posted a while ago. It has operators for possibility and necessity (<> and [], respectively). They bind to sub-expressions the same way negation (~) does; they bind to the nearest existential or universal quantifier to the right, or, failing that, the nearest predication to the right, so <>Px&Py is equivalent to (<>Px)&(Py) but not <>(Px&Py). <>x,Px&Py is equivalent to <>(x,Px&Py) but not (<>x,Px)&Py. I'm posting it and its source code, now that I have written a parser that I'm not ashamed of. The one downside is that it no longer supports the "old school" dot grouping. If any one wants to use it, tell me and I'll add it back in. If anyone uses this program at all, tell me!
- Download mpl.exe and some example logic files.
- Download the source code.
Labels:
UPL
Sunday, August 08, 2010
Monadic Predicate Logic
Suppose we restricted our thoughts to the concepts of something, everything, nothing, logical connectives like and, or, if...then or not, and monadic predicates, which are attributions of a property to an individual object, like "the sky is blue" or "tomorrow is Tuesday". (In the first statement, the sky is the object and blueness is its property. In the second statement, tomorrow is the object and being a Tuesday is its property. That's pretty restrictive, but it's enough to capture the logic behind such truths as the argument:
So why have I been explaining all this? Because I wrote a computer program that does just that. It's not the first to do so, and it only works for propositions that contain five or fewer predicates, but I spend a fair amount working on it, so I'm going to share it, anyway.
The Application
The application runs from the command line. It takes one or more text files as command-line arguments. When you execute it, it will read each file and try to interpret it as a statement of monadic predicate logic. If it can, it will decide whether the contents are necessarily true (valid), possibly true (valid only if additional premises were added), or self-contradictory (necessarily false).
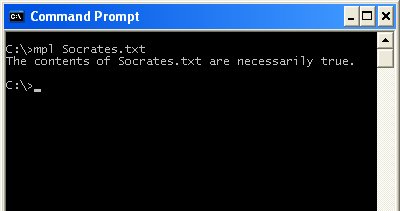
So, if I had an input file that contains the following text:
The Language
mpl.exe recognizes a particular language of symbolic logic. The language uses only ASCII characters available on American English keyboard. Its elements resemble either elements of ordinary symbolic logic or C-style bitwise operators. My intent is for the language to be unoriginal enough for someone who knows symbolic logic to be able to use it without much trouble. I'm too lazy to give a precise definition of the language, so I'll give a brief synopsis. If anyone has questions, I'll be happy to answer them.
The elements of the language are as follows:
The Algorithm
I won't say much about the algorithm right now, but I will say it is based on "possible worlds" semantics for logic. I will also say that it runs in O(2^n^n) time, where n is the number of predicates mentioned in a statement; it does not scale well. On my computer, mpl.exe finishes instantaneously for statements with three or fewer predicates and finishes in about a second for a statement with four predicates. I haven't tried it, but I estimate it would take about a day to finish evaluating a statement with five predicates. I didn't bother to implement mpl.exe in such a way that it would support more than five predicates, considering how long it would take to do that.
The Download
Click here to download the application.
The Future
I plan on extending mpl.exe to handle identity and modal operators for possibility and necessity. Maybe soon.
Socrates is a man.Which can be restated in a way that makes its logic more obvious:
Man is mortal.
Therefore, Socrates is mortal.
If Socrates is a man and if something is a man then it is mortal, then Socrates is mortal.The validity of any proposition that can be constructed from only the above-mentioned concepts is decidable. By "validity" I mean the proposition is true independent of anything else. "If something is both large and round, then it is large" is true whether or not anything large and/or round actually exists. The above-mentioned proof of Socrates' mortality is valid, too. By "proposition" I mean the meaning of a declarative, true-or-false statement. By "decidable" I mean someone could write a computer program that would the determine any one of these proposition's validity, and it would work for any proposition.
So why have I been explaining all this? Because I wrote a computer program that does just that. It's not the first to do so, and it only works for propositions that contain five or fewer predicates, but I spend a fair amount working on it, so I'm going to share it, anyway.
The Application
The application runs from the command line. It takes one or more text files as command-line arguments. When you execute it, it will read each file and try to interpret it as a statement of monadic predicate logic. If it can, it will decide whether the contents are necessarily true (valid), possibly true (valid only if additional premises were added), or self-contradictory (necessarily false).
So, if I had an input file that contains the following text:
// All men are mortal.I would test it through the command prompt like this:
x,Hx->Mx
// Socrates is a man.
Hs
// Therefore,
->
// Socrates is mortal.
Ms
The Language
mpl.exe recognizes a particular language of symbolic logic. The language uses only ASCII characters available on American English keyboard. Its elements resemble either elements of ordinary symbolic logic or C-style bitwise operators. My intent is for the language to be unoriginal enough for someone who knows symbolic logic to be able to use it without much trouble. I'm too lazy to give a precise definition of the language, so I'll give a brief synopsis. If anyone has questions, I'll be happy to answer them.
The elements of the language are as follows:
- Ax - a predicate, A, predicated on one variable x. Predicates can be any character from A to Z. Variables can be any character from a to z. These are what represents attributions of a property to an object. mpl.exe will handle statements with an unlimited number of these, so long as they use no more than five different predicates.
- (,) - grouping by parentheses, just like in algebra.
- .,:,:., etc. - old school grouping, like in Mathematical Logic.
- x,... - universal quantification, i.e. "for all x, ... is true". The generalization extends to the end of the group it is in, e.g. "x,Ax&y,By->Cx" means the same as "(x,Ax&(y,By->Cx))", but not the same as "(x,Ax)&(y,By->Cx)".
- 3x,... - existential quantification, i.e. "there is an x such that ... is true". It also extends to the end of the group it is in.
- ~... - negation.
- ...&.. - logical AND.
- ...|... - logical OR.
- ...->... - material conditional, i.e. IF...THEN...
- ...<=>... - logical equivalence. &,|,-> and <=> all have the same precedence and are left-associative.
- // ... - comments; anything after them is ignored by mpl.exe.
((x,Hx->Mx)&Hs)->MsThis is the basic categorical syllogism. You can add comments by adding "//" and text behind it:
((x,Hx->Mx)&Hs)->Ms //the basic categorical syllogismmpl.exe will ignore anything behind "//" . If a line only contains a comment, mpl.exe will ignore it completely:
// the basic categorical syllogismA statement can be spread across multiple lines. mpl.exe treats separate lines as if they were separate operand in a logical conjunction, so
((x,Hx->Mx)&Hs)->Ms
means the same asAx|BxBx->CxCx
(Ax|Bx)&(Bx->Cx)&(Cx)If a binary operator is on a line by itself, every line before it is conjoined and treated as its left operand; everything after it is conjoined and treated as its right operand. So
x,H->Mxmeans the same as
Hs
->
Ms
This allows us to symbolize logical arguments and test their validity. Think of the first two lines in the text above as the premises of an argument and the last line as the conclusion. As with computer programs, comments can be helpful:((x,Hx->Mx)&Hs)->Ms
// All men are mortal.
x,Hx->Mx
// Socrates is a man.
Hs
// Therefore,
->
// Socrates is mortal.
Ms
The Algorithm
I won't say much about the algorithm right now, but I will say it is based on "possible worlds" semantics for logic. I will also say that it runs in O(2^n^n) time, where n is the number of predicates mentioned in a statement; it does not scale well. On my computer, mpl.exe finishes instantaneously for statements with three or fewer predicates and finishes in about a second for a statement with four predicates. I haven't tried it, but I estimate it would take about a day to finish evaluating a statement with five predicates. I didn't bother to implement mpl.exe in such a way that it would support more than five predicates, considering how long it would take to do that.
The Download
Click here to download the application.
The Future
I plan on extending mpl.exe to handle identity and modal operators for possibility and necessity. Maybe soon.
Subscribe to:
Posts (Atom)